Markov
马尔可夫性质(Markov property)是指一个随机过程在给定现在状态及所有过去状态情况下,其未来状态的条件概率分布仅依赖于当前状态: $$ p\left(X_{t+1}=x_{t+1} \mid X_{0: t}=x_{0: t}\right)=p\left(X_{t+1}=x_{t+1} \mid X_t=x_t\right) $$
Markov Reward Process, MRP
在马尔可夫奖励过程中,状态转移矩阵和状态都与马尔可夫链一样,只是多了奖励函数(reward function)$ R $。它是一个期望,表示当我们到达某一个状态的时候,可以获得多大的奖励。
def
定义t时刻的回报(折扣回报)$ G_t=r_{t+1}+\gamma r_{t+2}+\gamma^2 r_{t+3}+\gamma^3 r_{t+4}+\ldots+\gamma^{T-t-1} r_T $,是一个随机变量。
def
定义回报的期望,即状态价值函数
$$ \begin{aligned} V^t(s) & =\mathbb{E}\left[G_t \mid s_t=s\right] \\ & =\mathbb{E}\left[r_{t+1}+\gamma r_{t+2}+\gamma^2 r_{t+3}+\ldots+\gamma^{T-t-1} r_T \mid s_t=s\right] \end{aligned} $$
计算价值函数的方法有多种,如下:
Monte Carlo, MC
生成很多轨迹,然把轨迹都叠加起来并取平均值。
Bellman equation
从价值函数出发,拆分出即时奖励和未来折扣奖励按概率的加权平均,得到贝尔曼方程:
$$ V(s)=\underbrace{R(s)}_{\text {即时奖励 }}+\underbrace{\gamma \sum _{s^{\prime} \in S} p\left(s^{\prime} \mid s\right) V\left(s^{\prime}\right)} _{\text {未来奖励的折扣总和 }} $$
这里$ R(s)=\mathbb{E}\left[r_{t+1} \mid s_t=s\right] $,具体证明见下方。
Lemma1 $$ \mathbb{E}\left[V\left(s_{t+1}\right) \mid s_t\right]=\mathbb{E}\left[\mathbb{E}\left[G_{t+1} \mid s_{t+1}\right] \mid s_t\right]=\mathbb{E}\left[G_{t+1} \mid s_t\right] $$ 第一个等号来自状态价值函数的定义,因此现在推导第二个等号。为记号简洁,将t时刻的量去掉下标,将t+1时刻的量去掉下标并加上标' $$ \begin{aligned} \mathbb{E}\left[\mathbb{E}\left[G_{t+1} \mid s_{t+1}\right] \mid s_t\right] & =\mathbb{E}\left[\mathbb{E}\left[g^{\prime} \mid s^{\prime}\right] \mid s\right] \\ & =\mathbb{E}\left[\sum_{g^{\prime}} g^{\prime} p\left(g^{\prime} \mid s^{\prime}\right) \mid s\right]\space (由条件期望定义) \\ & =\sum_{s^{\prime}} \sum_{g^{\prime}} g^{\prime} p\left(g^{\prime} \mid s^{\prime}, s\right) p\left(s^{\prime} \mid s\right)\space (由条件期望定义) \\ & =\sum_{s^{\prime}} \sum_{g^{\prime}} \frac{g^{\prime} p\left(g^{\prime} \mid s^{\prime}, s\right) p\left(s^{\prime} \mid s\right) p(s)}{p(s)}\space (补一个s的概率就可以用条件概率公式了!) \\ & =\sum_{s^{\prime}} \sum_{g^{\prime}} \frac{g^{\prime} p\left(g^{\prime} \mid s^{\prime}, s\right) p\left(s^{\prime}, s\right)}{p(s)}\space (由条件概率公式) \\ & =\sum_{s^{\prime}} \sum_{g^{\prime}} \frac{g^{\prime} p\left(g^{\prime}, s^{\prime}, s\right)}{p(s)} \\ & =\sum_{s^{\prime}} \sum_{g^{\prime}} g^{\prime} p\left(g^{\prime}, s^{\prime} \mid s\right)\space (由条件概率公式) \\ & =\sum_{g^{\prime}} \sum_{s^{\prime}} g^{\prime} p\left(g^{\prime}, s^{\prime} \mid s\right) \\ & =\sum_{g^{\prime}} g^{\prime} p\left(g^{\prime} \mid s\right) \\ & =\mathbb{E}\left[g^{\prime} \mid s\right]=\mathbb{E}\left[G_{t+1} \mid s_t\right] \end{aligned} $$
proof
$$ \begin{aligned} V(s) & = \mathbb{E}\left[G_t \mid s_t=s\right] \\ & = \mathbb{E}\left[r_{t+1}+\gamma r_{t+2}+\gamma^2 r_{t+3}+\ldots \mid s_t=s\right] \quad \text{(由回报定义)} \\ & = \mathbb{E}\left[r_{t+1} \mid s_t=s\right] + \gamma \mathbb{E}\left[r_{t+2}+\gamma r_{t+3}+\gamma^2 r_{t+4}+\ldots \mid s_t=s\right] \\ & = R(s) + \gamma \mathbb{E}\left[G_{t+1} \mid s_t=s\right] \\ & = R(s) + \gamma \mathbb{E}\left[V\left(s_{t+1}\right) \mid s_t=s\right] \quad \text{(由 Lemma 1)} \\ & = R(s) + \gamma \sum_{s^{\prime} \in S} p\left(s^{\prime} \mid s\right) V\left(s^{\prime}\right) \quad \text{(由条件期望定义)} \end{aligned} $$
大体思路就是将t时刻的V转化为G,利用期望的性质,拆分即时奖励和t+1时刻的G,再把G转化回V,从而得到V(s)与V(s’)的关系!
贝尔曼方程定义了当前状态与未来状态之间的迭代关系,表示当前状态的价值函数可以通过下个状态的价值函数来计算。因此在大多数情况下,贝尔曼方程的推导与计算确实是从后向前进行的,这意味着我们通常会从最末尾的状态开始往前计算状态的价值函数。
将所有状态的价值函数、即时奖励和状态之间的转移函数写为矩阵形式,可以直接得到解析解。但是状态数量较多时求解析解过于困难,因此往往采用其他的迭代方法! $$ \begin{aligned} &\begin{aligned} \boldsymbol{V} & =\boldsymbol{R}+\gamma \boldsymbol{P} \boldsymbol{V} \\ \boldsymbol{I} \boldsymbol{V} & =\boldsymbol{R}+\gamma \boldsymbol{P} \boldsymbol{V} \\ (\boldsymbol{I}-\gamma \boldsymbol{P}) \boldsymbol{V} & =\boldsymbol{R} \\ \boldsymbol{V} & =(\boldsymbol{I}-\gamma \boldsymbol{P})^{-1} \boldsymbol{R} \end{aligned} \end{aligned} $$
我们可以直接得到解析解(analytic solution):$ \boldsymbol{V}=(\boldsymbol{I}-\gamma \boldsymbol{P})^{-1} \boldsymbol{R} $
动态规划
通过自举 自举(bootstrapping) 方法不断迭代,当最后更新的状态和我们上一个状态的区别并不大的时候(收敛了),更新就可以停止。
Markov Decision Process,MDP
相对于马尔可夫奖励过程,马尔可夫决策过程多了决策(决策是指动作),其他的定义与马尔可夫奖励过程的是类似的。
def
定义策略为一个状态下可能采取动作的概率分布:$\pi (a|s)=p(a_t=a|s_t=s)$
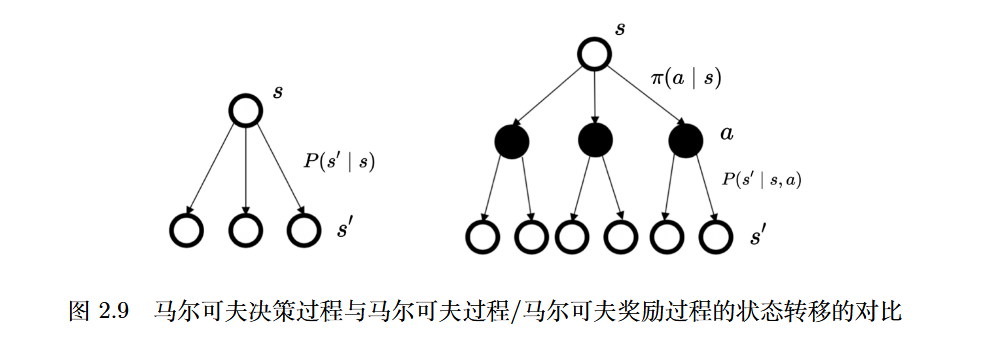
def
状态价值函数的定义与MRP形式相同,为$V_\pi(s)=\mathbb{E}_\pi\left[G_t \mid s_t=s\right]$。确定一个策略之后,对策略进行采样就可以得到期望。
def
引入Q函数,定义为在某一个状态采取某一个动作下回报的期望,即$Q_\pi(s,a)=\mathbb{E}_\pi\left[G_t \mid s_t=s,a_t=a\right]$
自然就有V与Q的关系: $$ V_\pi(s)=\sum_{a \in A} \pi(a \mid s) Q_\pi(s, a) $$
Bellman equation
形式与MRP仍然是类似的!只是多了动作 $ a $ : $$ \begin{aligned} Q(s, a) & =\mathbb{E}\left[G_t \mid s_t=s, a_t=a\right] \\ & =\mathbb{E}\left[r_{t+1}+\gamma r_{t+2}+\gamma^2 r_{t+3}+\ldots \mid s_t=s, a_t=a\right] \\ & =\mathbb{E}\left[r_{t+1} \mid s_t=s, a_t=a\right]+\gamma \mathbb{E}\left[r_{t+2}+\gamma r_{t+3}+\gamma^2 r_{t+4}+\ldots \mid s_t=s, a_t=a\right] \\ & =R(s, a)+\gamma \mathbb{E}\left[G_{t+1} \mid s_t=s, a_t=a\right] \\ & =R(s, a)+\gamma \mathbb{E}\left[V\left(s_{t+1}\right) \mid s_t=s, a_t=a\right] \\ & =R(s, a)+\gamma \sum_{s^{\prime} \in S} p\left(s^{\prime} \mid s, a\right) V\left(s^{\prime}\right) \end{aligned} $$
Bellman expectation equation
结合V与Q的关系,代入Bellman equation,分别得到s与s’时刻V和Q的关系: $$ V_\pi(s)=\sum_{a \in A} \pi(a \mid s)\left(R(s, a)+\gamma \sum_{s^{\prime} \in S} p\left(s^{\prime} \mid s, a\right) V_\pi\left(s^{\prime}\right)\right) $$
$$ Q_\pi(s, a)=R(s, a)+\gamma \sum_{s^{\prime} \in S} p\left(s^{\prime} \mid s, a\right) \sum_{a^{\prime} \in A} \pi\left(a^{\prime} \mid s^{\prime}\right) Q_\pi\left(s^{\prime}, a^{\prime}\right) $$
备份图
分别从图形角度解释了Bellman expectation equation!
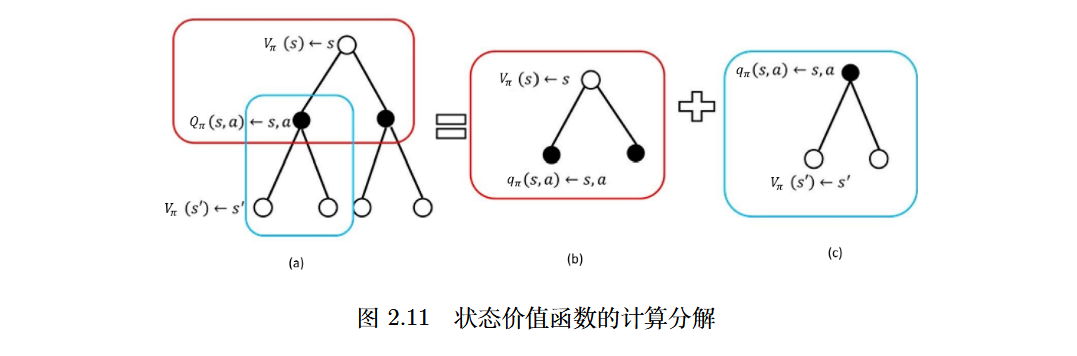
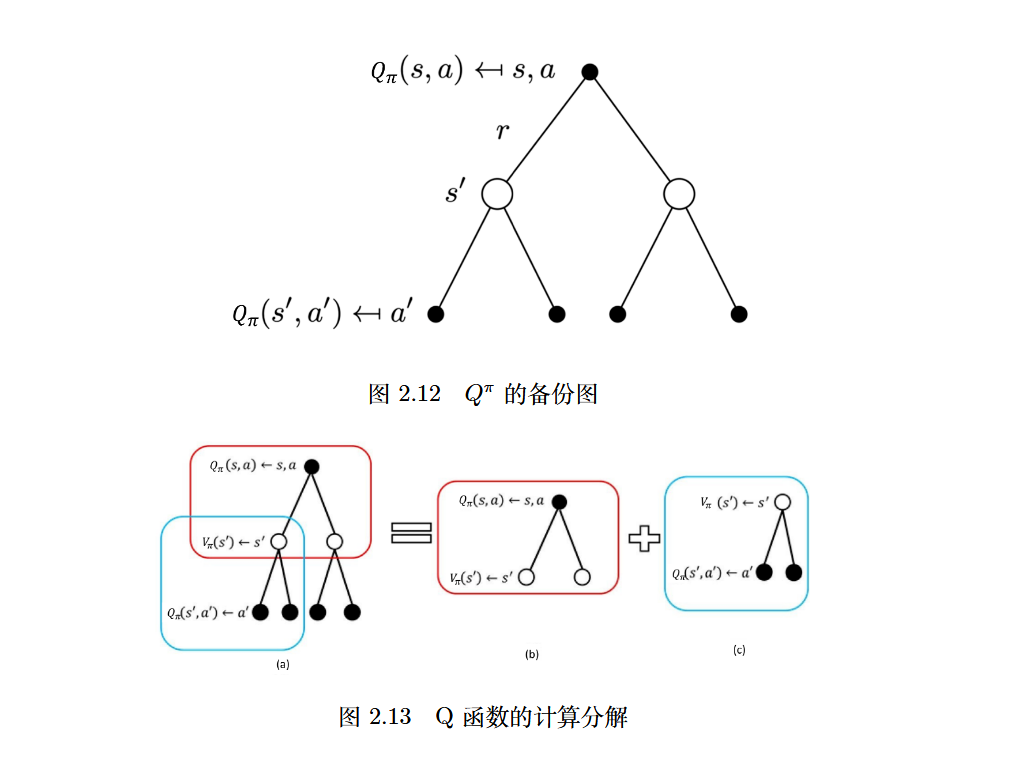
预测与控制
- 预测(评估一个给定的策略)的输入是马尔可夫决策过程$< S,A,P,R,\gamma>$和策略$π$,输出是价值函数$V_π$。预测是指给定一个马尔可夫决策过程以及一个策略$π$,计算它的价值函数,也就是计算每个状态的价值。
- 控制(搜索最佳策略)的输入是马尔可夫决策过程$<S,A,P,R,\gamma>$,输出是最佳价值函数(optimal value function)$ V^* $和最佳策略(optimal policy)$ π^* $。控制就是我们去寻找一个最佳的策略,然后同时输出它的最佳价值函数以及最佳策略。
实际上,这两者是递进的关系,在强化学习中,我们通过解决预测问题,进而解决控制问题。
搜索最佳策略的方法
对于控制而言,要找出最佳策略,通用有两种方法。
-
策略迭代
对目前已优化出来的最新策略,计算状态价值函数,并进一步推算Q函数。对Q函数进行最大化,用贪心搜索改进策略。以此类推,逐步迭代。
$$ Q_{\pi_i}(s, a)=R(s, a)+\gamma \sum_{s^{\prime} \in S} p\left(s^{\prime} \mid s, a\right) V_{\pi_i}\left(s^{\prime}\right) $$
$$ \pi_{i+1}(s)=\underset{a}{\arg \max } Q_{\pi_i}(s, a) $$

- Bellman optimality equation:最佳策略下的一个状态的价值必须等于在这个状态下采取最好动作得到的回报的期望
$$ V_\pi(s)=\max_{a \in A} Q_\pi(s, a) $$
只有当整个状态已经收敛后,我们得到最佳价值函数后,贝尔曼最优方程才会满足。满足贝尔曼最优方程后,我们可以采用最大化操作,即
$$ V^*(s)=\max_{a} Q^*(s, a) $$
因此,可以得到Q函数之间的转移:
$$ \begin{aligned} Q^*(s, a) & =R(s, a)+\gamma \sum_{s^{\prime} \in S} p\left(s^{\prime} \mid s, a\right) V^*\left(s^{\prime}\right) \\ & =R(s, a)+\gamma \sum_{s^{\prime} \in S} p\left(s^{\prime} \mid s, a\right) \max _a Q^*\left(s^{\prime}, a^{\prime}\right) \end{aligned} $$
类似也有状态价值函数之间的转移:
$$ \begin{aligned} V^*(s) & =\max _a Q^*(s, a) \\ & =\max _a R(s, a)+\max _a \gamma \sum _{s^{\prime} \in S} p\left(s^{\prime} \mid s, a\right) V^*\left(s^{\prime}\right) \\ & =\max _a\left(R(s, a)+\gamma \sum _{s^{\prime} \in S} p\left(s^{\prime} \mid s, a\right) V^*\left(s^{\prime}\right)\right) \end{aligned} $$
-
价值迭代
最优性原理定理(principle of optimality theorem):一个策略 $\pi(a \mid s)$ 在状态 $s$ 达到了最优价值,也就是 $V_\pi(s)=V^*(s)$ 成立,当且仅当对于任何能够从 $s$ 到达的 $s^{\prime}$ ,都已经达到了最优价值。也就是对于所有的 $s^{\prime}, V_\pi\left(s^{\prime}\right)=V^*\left(s^{\prime}\right)$ 恒成立。
有点乱,待重看!

表格型方法
免模型预测
-
蒙特卡洛方法:为了得到评估 $V(s)$ ,我们采取了如下的步骤。 (1)在每个回合中,如果在时间步 $t$ 状态 $s$ 被访问了,那么 -状态 $s$ 的访问数 $N(s)$ 增加 $1, N(s) \leftarrow N(s)+1$ 。 -状态 $s$ 的总的回报 $S(s)$ 增加 $G_t, S(s) \leftarrow S(s)+G_t$ 。 (2)状态 $s$ 的价值可以通过回报的平均来估计,即 $V(s)=S(s) / N(s)$ 。 根据大数定律,只要我们得到足够多的轨迹,就可以趋近这个策略对应的价值函数。当 $N(s) \rightarrow \infty$时,$V(s) \rightarrow V_\pi(s)$ 。
-
增量式蒙特卡洛(incremental MC)方法
假设现在有样本 $x_1, x_2, \cdots, x_t$ ,我们可以把经验均值(empirical mean)转换成增量均值(incremental mean)的形式: $$ \begin{aligned} \mu_t & =\frac{1}{t} \sum_{j=1}^t x_j \\ & =\frac{1}{t}\left(x_t+\sum_{j=1}^{t-1} x_j\right) \\ & =\frac{1}{t}\left(x_t+(t-1) \mu_{t-1}\right) \\ & =\frac{1}{t}\left(x_t+t \mu_{t-1}-\mu_{t-1}\right) \\ & =\mu_{t-1}+\frac{1}{t}\left(x_t-\mu_{t-1}\right) \end{aligned} $$
通过这种转换,我们就可以把上一时刻的平均值与现在时刻的平均值建立联系,即
$$ \mu_t=\mu_{t-1}+\frac{1}{t}\left(x_t-\mu_{t-1}\right) $$ 其中,$x_t-\mu _{t-1}$是残差,$\frac1{t}$类似于学习率。当我们得到$x_t$时,就可以利用上一时刻的值来更新现在的值。
- 时序差分
策略梯度
$r(s,a)$:即时奖励,描述在某个状态 $s$ 下执行动作 $a$ 时,环境立即返回的奖励(一个瞬时的值)。
$R(τ)$:轨迹奖励,表示一条完整轨迹 $\tau$ 的累积奖励,即所有时间步的即时奖励的代数和: $$ R(\tau) = \sum_{t=0}^T r(s_t, a_t) $$ 因此,给定一个策略 $\theta$ ,就可以计算期望奖励: $$ \bar{R}_\theta = \sum _\tau R(\tau) p _\theta(\tau)=\mathbb{E} _{\tau \sim p _\theta(\tau)}[R(\tau)] $$
梯度上升
进行梯度上升,我们先要计算期望奖励 $\bar{R}\theta$ 的梯度。我们对 $\bar{R}\theta$ 做梯度运算 $$ \nabla \bar{R}_\theta=\sum _\tau R(\tau) \nabla p _\theta(\tau) $$
其中,只有 $p_\theta(\tau)$ 与 $\theta$ 有关。奖励函数 $R(\tau)$ 不需要是可微分的(differentiable)。
直观理解
- $R(\tau)$ 相当于给每条轨迹打分,是一个固定的分数,已经由环境和轨迹决定好了。
- 梯度上升的目标是通过调整 $\theta$ 改变 $p_\theta(\tau)$,使得高分轨迹(高 $R(\tau)$)的概率变大,低分轨迹的概率变小。
数学处理
观察到$p_{\theta}(\tau)$中有冗长的条件概率的乘积,自然想到取对数。这样做可以有效的将转化为加和,简单化处理。
类似链式求导法则,有公式: $$ \nabla f(x)=f(x) \nabla \log f(x) $$
从而得到 $\nabla p_\theta(\tau)=p_\theta(\tau) \nabla \log p_\theta(\tau)$ 。然后看看取对数的威力: $$ \begin{aligned} \nabla \log p_\theta(\tau) & =\nabla\left(\log p\left(s_1\right)+\sum_{t=1}^T \log p_\theta\left(a_t \mid s_t\right)+\sum_{t=1}^T \log p\left(s_{t+1} \mid s_t, a_t\right)\right) \\ & =\nabla \log p\left(s_1\right)+\nabla \sum_{t=1}^T \log p_\theta\left(a_t \mid s_t\right)+\nabla \sum_{t=1}^T \log p\left(s_{t+1} \mid s_t, a_t\right) \\ & =\nabla \sum_{t=1}^T \log p_\theta\left(a_t \mid s_t\right) \\ & =\sum_{t=1}^T \nabla \log p_\theta\left(a_t \mid s_t\right) \end{aligned} $$
注意,$p\left(s_1\right)$ 和 $p\left(s_{t+1} \mid s_t, a_t\right)$ 来自环境,$p_\theta\left(a_t \mid s_t\right)$ 来自智能体。 $p\left(s_1\right)$ 和 $p\left(s_{t+1} \mid s_t, a_t\right)$ 由环境决定,与 $\theta$ 无关,因此 $\nabla \log p\left(s_1\right)=0, ~ \nabla \sum_{t=1}^T \log p\left(s_{t+1} \mid s_t, a_t\right)=0$ 。
接下来,就可以代入梯度运算啦: $$ \begin{aligned} \nabla \bar{R}_\theta & =\sum _\tau R(\tau) \nabla p _\theta(\tau) \\ & =\sum _\tau R(\tau) p _\theta(\tau) \frac{\nabla p _\theta(\tau)}{p _\theta(\tau)} \\ & =\sum _\tau R(\tau) p _\theta(\tau) \nabla \log p _\theta(\tau) \\ & =\mathbb{E} _{\tau \sim p _\theta(\tau)}\left[R(\tau) \nabla \log p _\theta(\tau)\right] \\ & \approx \frac{1}{N} \sum _{n=1}^N R\left(\tau^n\right) \nabla \log p _\theta\left(\tau^n\right) \\ & =\frac{1}{N} \sum _{n=1}^N \sum _{t=1}^{T_n} R\left(\tau^n\right) \nabla \log p _\theta\left(a _t^n \mid s _t^n\right) \end{aligned} $$
实际上期望值 $\mathbb{E} _{\tau \sim p _\theta(\tau)}\left[R(\tau) \nabla \log p _\theta(\tau)\right]$ 无法计算,只能用样本来估计了!所以最后两步是在用采样的方式采样 $N$ 个 $\tau$ 并计算每一个的值。
实现技巧
基线
梯度上升是让高分轨迹上升,怎么评判是否为高分呢?目前似乎就是看 $\tau$ 这条轨迹的累计奖励是否为正,为正则提高其概率。
这不好,有的情景设置所有即时奖励都是正的,这种情况下任何一条轨迹的累计奖励都是正的,就大错特错咯。
为了解决奖励总是正的的问题,我们可以把奖励减 $b$ (可取期望),即 $$ \begin{aligned} \nabla \bar{R}_\theta & \approx\frac{1}{N} \sum _{n=1}^N \sum _{t=1}^{T_n} (R\left(\tau^n\right)-b) \nabla \log p _\theta\left(a_t^n \mid s_t^n\right) \end{aligned} $$
分数分配
为什么一定要选 $R(\tau ^n))$ 作为权重呢?对于一个动作来说,它之前发生的事对于奖励的贡献和它完全无关。那就从 $t$ 时刻开始计算权重吧,再加一个折扣: $$ \begin{aligned} \nabla \bar{R}_\theta & \approx\frac{1}{N} \sum _{n=1}^N \sum _{t=1}^{T_n} (\sum _{t^\prime=t}^{T_n} \gamma^{t^\prime-t}r _{t^\prime}^n-b) \nabla \log p _\theta\left(a_t^n \mid s_t^n\right) \end{aligned} $$
深度Q网络
学习过程
根据一个策略 $\pi$ ,得到其Q函数。然后得到一个更好的策略 $\pi^\prime$, $$ \pi^{\prime}(s)=\underset{a}{\arg \max } Q_\pi(s, a) $$ 可以证明这个策略是更好的,首先有 $$ V_\pi(s)=Q_\pi(s,\pi(s))\le \underset{a}{\max}Q_\pi(s,a)=Q_\pi(s,\pi^\prime(s)) $$ 虽然只有一步之差,除了这一步以外全部都一样(都按照$\pi$选动作),但是在这一步我按照$\pi^\prime$选动作就是更好!因此只需证: $$ Q_\pi(s,\pi^\prime(s))\le V_{\pi\prime}(s) $$ 既然只一步不一样就可以变好,那假设每一步都不一样,还会变得更好!如下: $$ \begin{aligned} Q_\pi\left(s, \pi^{\prime}(s)\right) &=\mathbb{E}\left[r_t+V_\pi\left(s_{t+1}\right) \mid s_t=s, a_t=\pi^{\prime}\left(s_t\right)\right] \\ & \leq \mathbb{E}\left[r_t+Q^\pi\left(s_{t+1}, \pi^{\prime}\left(s_{t+1}\right)\right) \mid s_t=s, a_t=\pi^{\prime}\left(s_t\right)\right] \\ & =\mathbb{E}\left[r_t+r_{t+1}+V^\pi\left(s_{t+2}\right) \mid s_t=s, a_t=\pi^{\prime}\left(s_t\right)\right] \\ & \leq \mathbb{E}\left[r_t+r_{t+1}+Q^\pi\left(s_{t+2}, \pi^{\prime}\left(s_{t+2}\right) \mid s_t=s, a_t=\pi^{\prime}\left(s_t\right)\right]\right. \\ & =\mathbb{E}\left[r_t+r_{t+1}+r_{t+2}+V^\pi\left(s_{t+3}\right) \mid s_t=s, a_t=\pi^{\prime}\left(s_t\right)\right] \\ & \leq \cdots \\ & \leq \mathbb{E}\left[r_t+r_{t+1}+r_{t+2}+\cdots \mid s_t=s, a_t=\pi^{\prime}\left(s_t\right)\right] \\ & =V^{\pi^{\prime}}(s) \end{aligned} $$
技巧
Target Network
目标网络的核心思想是:分离估计值和目标值,降低训练的不稳定性。在 DQN 中,它的作用是:
- 估计 Q 值时,目标 y 由 一个较老的 Q 网络(目标网络) 计算,而不是使用正在训练的主网络。
- 目标网络的参数 每隔一段时间才更新,而不是每次更新都改变它。
这个技巧可以减少训练时的 自相关性(correlation) 和 目标值剧烈变化 导致的不稳定性。
与之前学习的n-step TD,SARSA都有共同的思想
Exploration
例如,假设我们用深度 Q 网络来玩 slither.io 网页游戏。我们有一条蛇,它在环境里面走来走去,吃到星星,就加分。假设游戏一开始,蛇往上走,然 后吃到星星,就可以得到分数,它就知道往上走可以得到奖励。接下来它就再也不会采取往上走以外的动 作了,以后就会变成每次游戏一开始,它就往上走,然后游戏结束。所以需要有探索的机制,让智能体知 道,虽然根据之前采样的结果,a2 好像是不错的,但我们至少偶尔也试一下 a1 与 a3,说不定它们更好。
这个问题就是 探索-利用窘境(exploration-exploitation dilemma) 问题
一种方法是$\epsilon$-贪心,即每次有一定概率随机探索,其他情况下按照Q函数来决定动作;另一种是玻尔兹曼探索,在探索时不像前者那样均匀地探索,而是有一定说法: $$ \pi(a \mid s)=\frac{\mathrm{e}^{Q(s, a) / T}}{\sum_{a^{\prime} \in A} \mathrm{e}^{Q\left(s, a^{\prime}\right) / T}} $$ 可以看到,
高温(T 大)→ 均匀探索:
- $e^{Q(a)/T}$ 变得相近,每个动作的概率接近。
- 例如 T=1000T=1000T=1000 时,所有动作几乎等概率选择,接近纯随机探索。
低温(T 小)→ 接近贪心策略:
- $e^{Q(a)/T}$ 变得差距很大,较优的动作概率接近 1,劣势动作趋向 0。
- 例如 T=0.01T=0.01T=0.01 时,几乎总是选择 Q 值最高的动作(接近贪心)。
一个很形象的类比:
- ε-贪心 就像 赌徒,90% 的时候去玩最赚钱的老虎机,10% 完全随机换一台试试。
- 玻尔兹曼 就像 股票投资者,越是有收益的股票,投资的概率越大,但不会全压在一只股票上,而是有一定分布。
Experience Replay
构建一个Replay Buffer, 用来在更新策略的过程中,收集一连串变化的策略分别得到的数据,作为经验集。然后再均匀地从中进行采样,替代原来与环境交互采样的方式。
因此,使用这个技巧会使得算法变为异策略的。因为Q本来是要观察 π 的经验的,但实际上存储在回放缓冲区里面的这些经验不是通通来自于 π。
好处是节约了与环境交互的次数(这部分往往是最耗时的),同时增加了数据的多样性,避免同质化影响训练质量。
Prioritized ER
均匀地从回放缓冲区中采样数据也不一定最好,有些数据可能更加重要!
如果发现某些已采样过的数据的时序差分误差特别大(训练的网络输出和目标之间的差值大),说明网络训练的不理想,需要多加训练。因此,对这类数据基于优先权~
Double DQN
在实现上,Q 值往往是被高估的,使用
$$ Q\left(s_t, a_t\right) \longleftrightarrow r_t+\max _a Q\left(s _{t+1}, a\right) $$
作为目标,会使得网络估计的Q值太高,因此DDQN设置了两个网络,一个用来选动作,另一个用来计算目标:
$$ Q\left(s_t, a_t\right) \longleftrightarrow r_t+Q^\prime(s _{t+1},\underset{a}{\arg \max}\space Q\left(s _{t+1}, a\right)) $$
加入Q高估了选出来的动作a,只要Q’没有高估a对应的Q值就可以;加入Q’高估了某个的动作a,只要Q没有选择这个动作就可以。而且,这一操作对于DQN的更改是最少的,几乎没有增加任何运算量!
Dueling DQN
与DQN不同,Dueling DQN会拆分成两条路径运算,分别给出一个标量 $V(s)$ 和一个向量 $A(s, a)$,后者叫优势函数。
相加再得到 $Q(s,a)$:
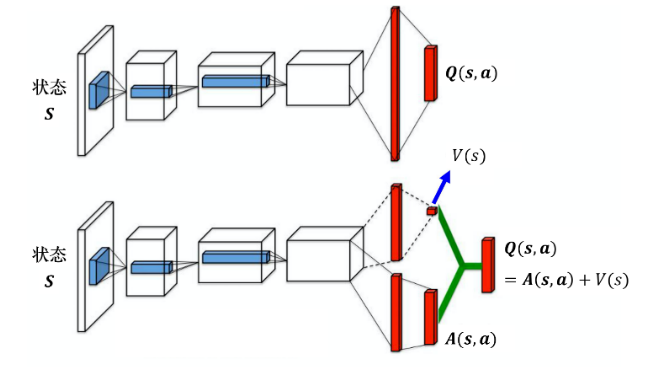
- 约束:固定 $s$ 不变,$\sum_{a}A(s,a)=0$
- 实现方法:加入归一化过程(计算均值并减去均值)
- 好处:通过更改 $V(s)$ 间接修改那些没有被采样到的 $(s, a)$ 对的Q值,让学习更加稳定、高效!
Noisy Net
每回合智能体要与环境交互时,给Q网络的每一个参数加上一个高斯噪声得到 $\tilde Q$, $$ a=\underset{a}{\arg \max } \tilde{Q}(s, a) $$ 直到回合结束,这个噪声都不改变,以确保对于同一状态,智能体有一致的相应。
Distributional Q-function
Q函数是累计奖励的期望值,也就是对于一个分布取了平均值。但不同分布可以有同样的均值,因此Q值似乎会损失一些信息。
如果直接对分布建模,每一个状态动作对都能得到一个分布,就可以有更多选择,如:
“如果分布 方差很大,这代表采取这个动作虽然平均而言很不错,但也许风险很高,我们可以训练一个网络来规避风险。在两个动作平均值都差不多的情况下,也许可以选一个风险比较小的动作来执行”
但这一技巧难以实现。
针对连续动作的方案
采样
显然,采样N个可能的动作并分别计算Q值是可行的,而且不会太低效。但很明显这不是很精确~
梯度上升
既然要解决的是一个优化问题(optimization problem),我们就要最大化目标函数(objective function)。要最大化目标函数,我们就可以用梯度上升。
但有如下两个问题:
- Q 函数可能是 非凸 的,梯度上升可能会停在局部最优,而不是全局最优。
- 运算量很大:每次决定采取哪一个动作的时候,还要训练一次网络,迭代地更新 。
设计网络架构
调整网络架构:输入 $s, \mathrm{Q}$ 函数会输出向量 $\boldsymbol{\mu}(\boldsymbol{s})$ ,正定矩阵 $\boldsymbol{\Sigma}(\boldsymbol{s})$ 和标量 $V(\boldsymbol{s})$ 。 Q 函数根据输人 $\boldsymbol{s}$ 与 $\boldsymbol{a}$ 来决定输出值。到目前为止, Q 函数只有输入$s$ ,它还没有输入 $\boldsymbol{a}, \boldsymbol{a}$ 在哪里呢?接下来我们可以输入$\boldsymbol{a}$ ,用 $\boldsymbol{a}$ 与 $\boldsymbol{\mu}(s), ~ \Sigma(s)$ 和 $V(s)$ 互相作用。 Q 函数可定义为
$$ Q(s, a)=-(\boldsymbol{a}-\boldsymbol{\mu}(\boldsymbol{s}))^{\mathrm{T}} \boldsymbol{\Sigma}(\boldsymbol{s})(\boldsymbol{a}-\boldsymbol{\mu}(\boldsymbol{s}))+V(\boldsymbol{s}) $$ 由正定矩阵性质 $x^TAx > 0$ ,可知要最大化Q函数,只需令 $\boldsymbol{\mu}(\boldsymbol{s})$ 等于 $\boldsymbol{a}$ 。
演员-评论员算法
优势演员-评论员算法
从策略梯度应用基线技巧的结果出发: $$ \begin{aligned} \nabla \bar{R}_\theta & \approx\frac{1}{N} \sum _{n=1}^N \sum _{t=1}^{T_n} (R\left(\tau^n\right)-b) \nabla \log p _\theta\left(a_t^n \mid s_t^n\right) \end{aligned} $$
常用价值函数 $V_{\pi_\theta}\left(s_t^n\right)$ 来表示基线。 $V_{\pi_\theta}\left(s_t^n\right)$ 没有涉及动作,$Q_{\pi_\theta}\left(s_t^n, a_t^n\right)$ 涉及动作。
$V_{\pi_\theta}\left(s_t^n\right)$ 是 $Q_{\pi_\theta}\left(s_t^n, a_t^n\right)$ 的期望值,$Q_{\pi_\theta}\left(s_t^n, a_t^n\right)-V_{\pi_\theta}\left(s_t^n\right)$ 会有正有负,所以 $\sum_{t^{\prime}=t}^{T_n} \gamma^{t^{\prime}-t} r_{t^{\prime}}^n-b$ 这一项就会有正有负。
所以我们就把策略梯度里面 $\sum_{t^{\prime}=t}^{T_n} \gamma^{t^{\prime}-t} r_{t^{\prime}}^n-b$ 这一项换成了优势函数 $A^\theta\left(s_t^n, a_t^n\right)$ ,即 $Q_{\pi_\theta}\left(s_t^n, a_t^n\right)-V_{\pi_\theta}\left(s_t^n\right)$
这么实现有一个缺点,即我们需要估计两个网络,估计不准的风险就变成原来的两倍。事实上,在演员-评论员算法中,我们可以只估计网络 V ,并利用 $V$ 的值来表示 $Q$ 的值,在Bellman Equation部分证明过$Q_\pi\left(s_t^n, a_t^n\right)$ 和 $V_\pi\left(s_{t+1}^n\right)$ 的关系,即 $$ Q_\pi\left(s_t^n, a_t^n\right)=\mathbb{E}\left[r_t^n+V_\pi\left(s_{t+1}^n\right)\right] $$
现在把取期望值去掉(你别管能不能去,论文说这个最好那它就是可行的),即
$$ Q_\pi\left(s_t^n, a_t^n\right)=r_t^n+V_\pi\left(s_{t+1}^n\right) $$
我们就可以把 Q 函数的值用 $r_t^n+V_\pi\left(s_{t+1}^n\right)$ 取代,可得
$$ \begin{aligned} \nabla \bar{R}_\theta & \approx\frac{1}{N} \sum _{n=1}^N \sum _{t=1}^{T_n} (r_t^n+V _\pi\left(s _{t+1}^n\right)-V _\pi\left(s_t^n\right)) \nabla \log p _\theta\left(a_t^n \mid s_t^n\right) \end{aligned} $$
深度确定性策略梯度
从名字拆解出关键词:深度+确定性+策略梯度
将深度Q网络扩展到连续空间,借鉴了其技巧:目标网络和经验回放
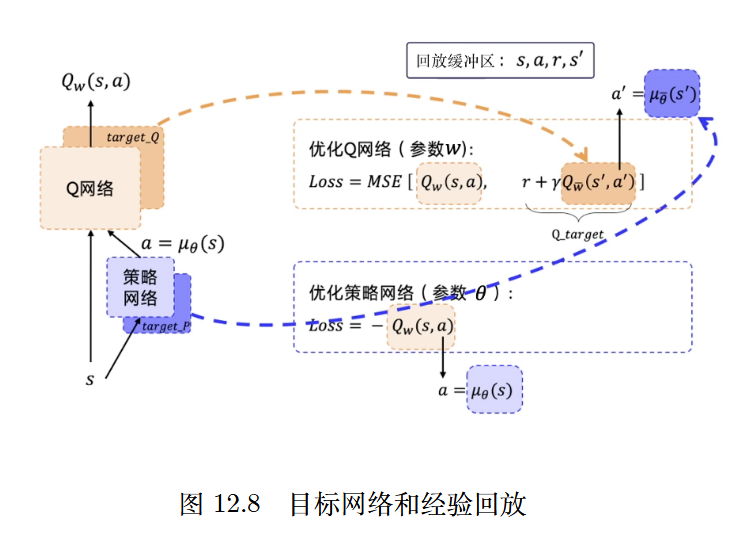
DDPG 的原作者推荐使用时间相关的 OU 噪声,但最近的结果表明不相关的、均值为 0 的高斯噪声的效果非常好。由于后者更简单,因此我们更喜欢使用它。为了便于获得更高质量的训练数据,我们可以在训练过程中把噪声变小。
