在本课程Unit1中,我们需要迭代开发一个表达式化简的程序,最终实现展开括号、支持函数、支持求导等功能。
程序架构度量分析与设计体验
先导课和单元实验已经引导我们认识了递归下降的架构,我认为其在解析表达式方面功能强大,且其高扩展性可以应对迭代开发中可能产生的额外需求,所以我在第一次作业时果断选择了沿用这一架构。
第一次作业
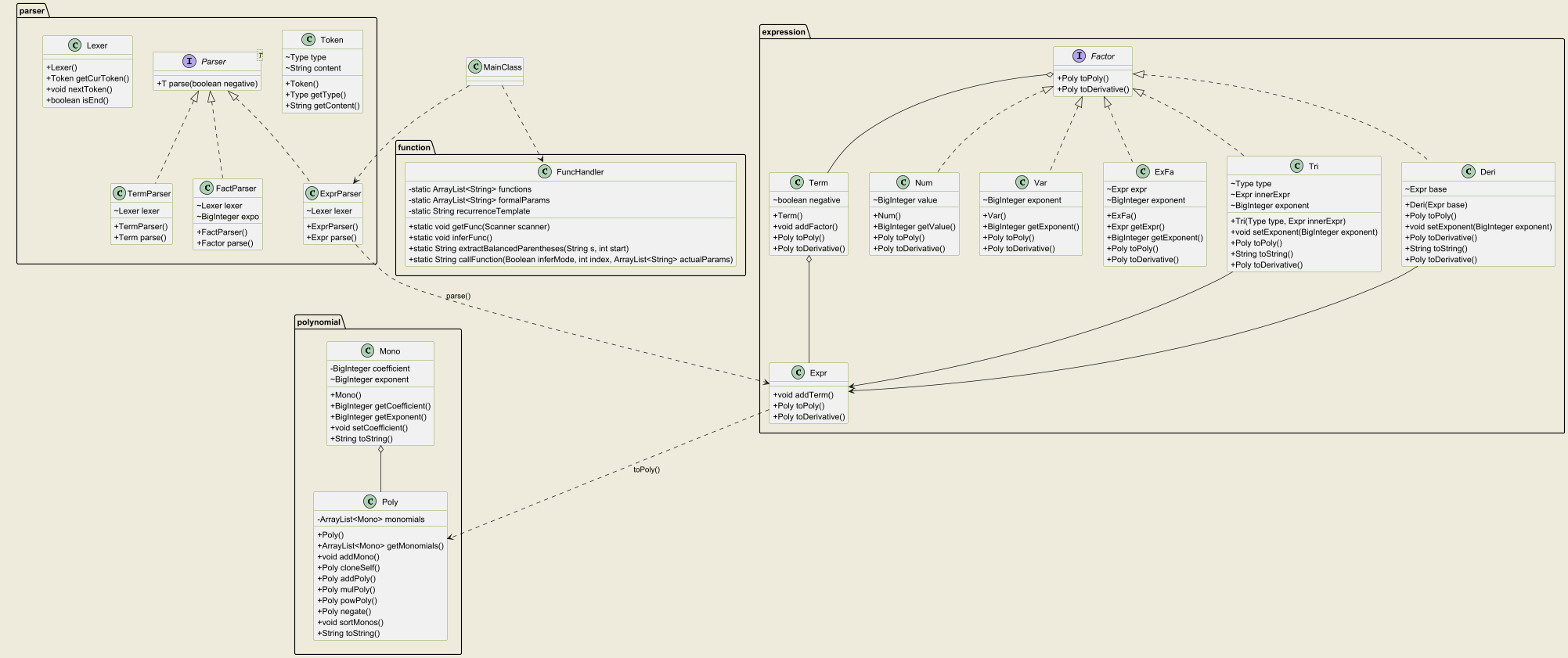
第一次作业需求较为简单,我将程序主体部分分为3个包:parser、expression和polynomial,功能分别是:
-
用递归下降的方法解析待化简字符串。
-
按照形式化定义设置了
Expr类、Term类和Factor接口(当前有Num、Var和ExFa三个类实现),接受解析得到的结果。 -
应用归一化的思想,将
expression包中的各类转化为统一的单项式、多项式,方便化简及后续增添功能。Poly中使用ArrayList存储各单项式,Mono的形式均规定为: $$ \text{Mono}=a*x^b $$
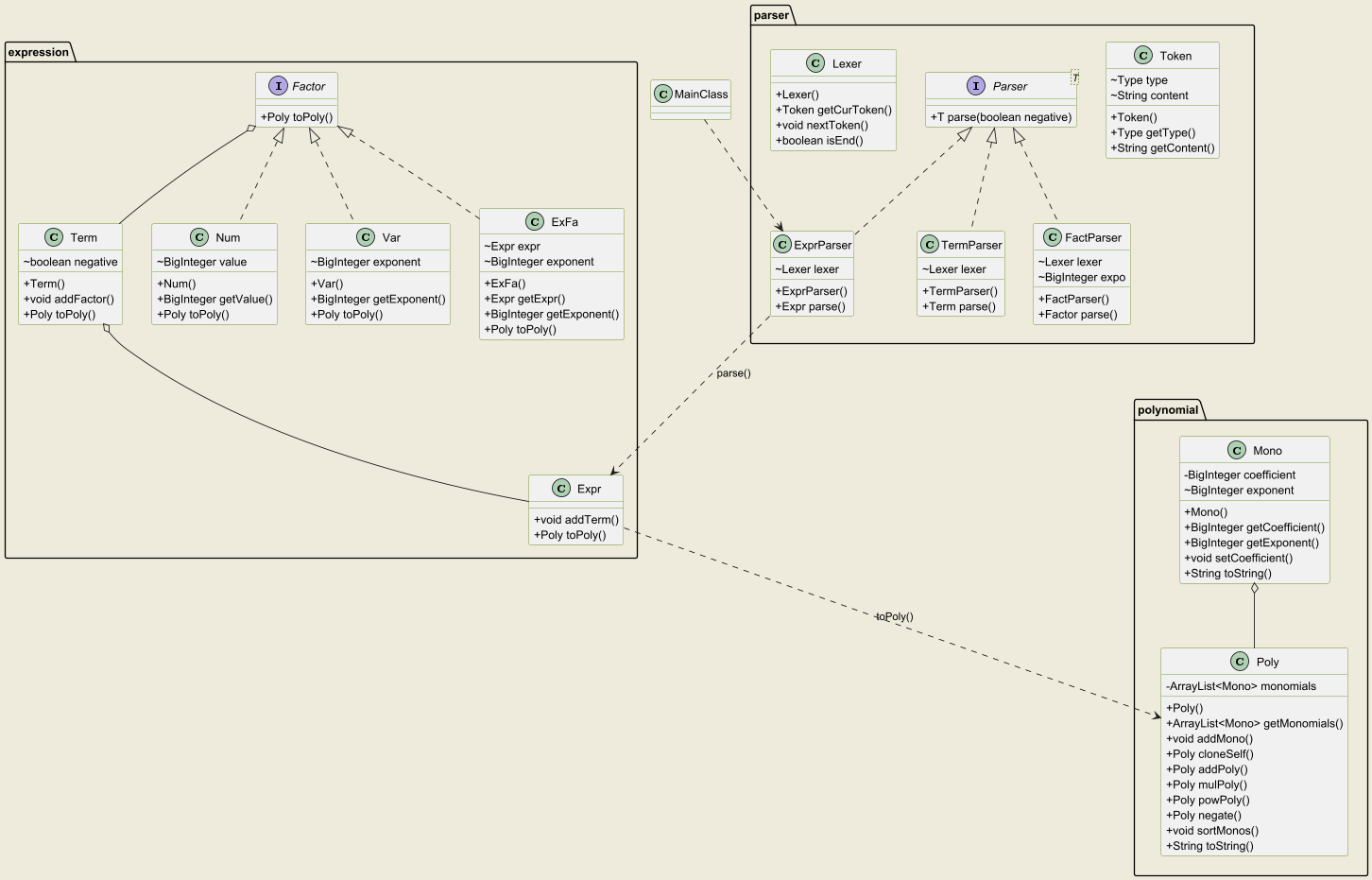
分析本次作业复杂度,可以明显看到本次作业中Lexer和FactParser类中的主要方法过于复杂,我认为主要是因为这两个类都涉及了多种输入类型的处理,逻辑复杂且耦合度较高。
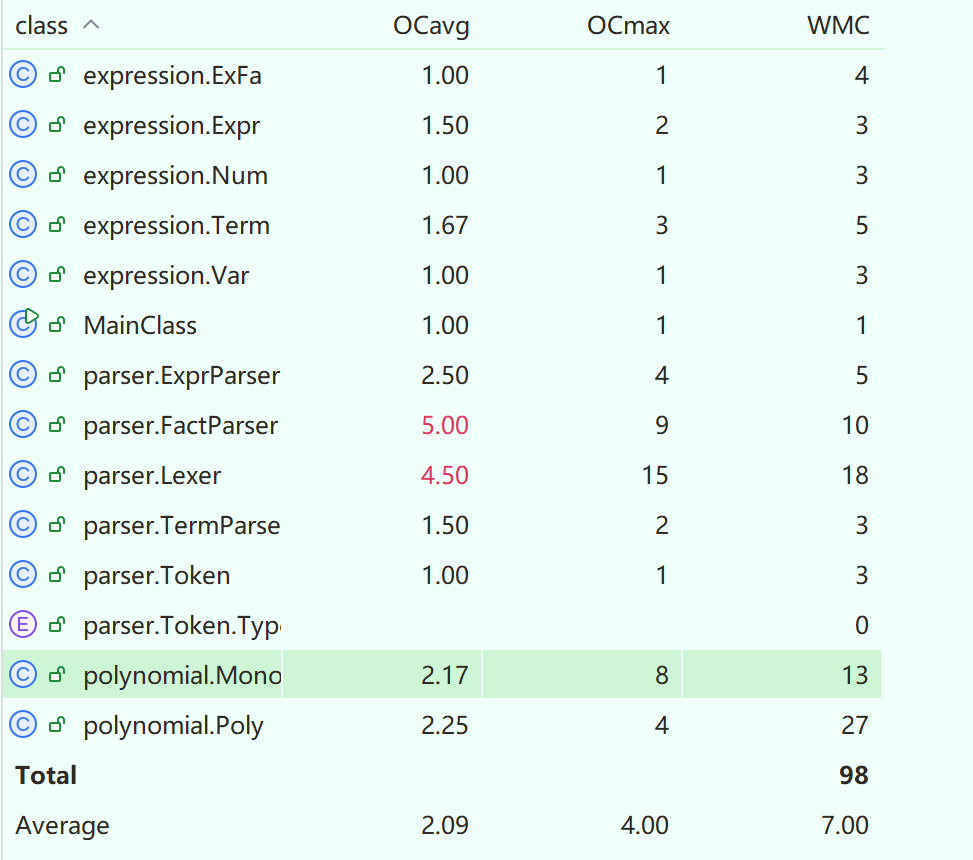
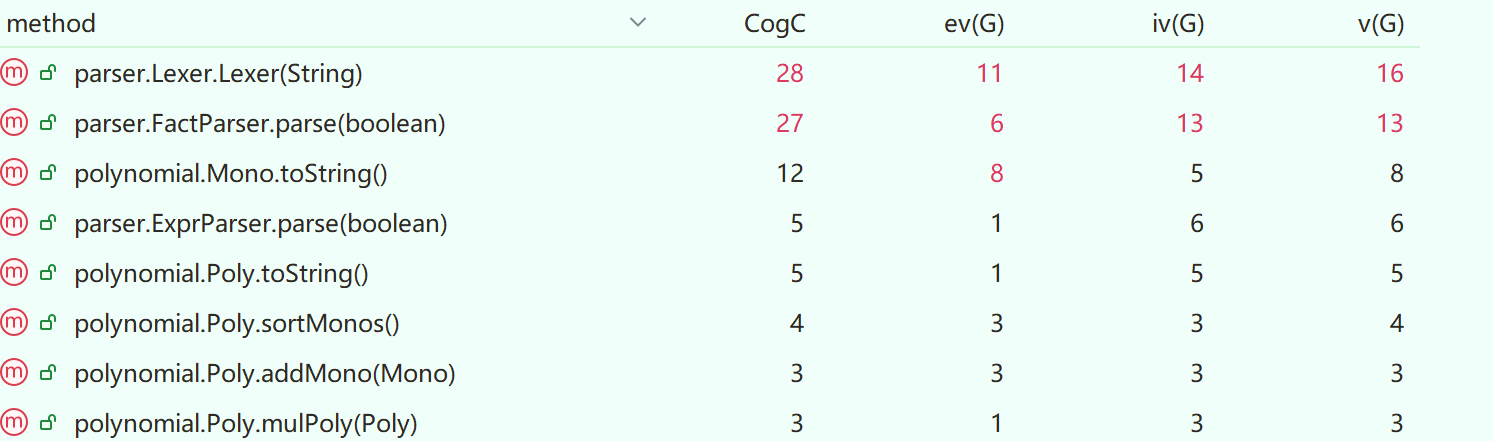
第二次作业
由于第一次作业架构可扩展性较高,后续作业中我都没有进行重构。面对第二次作业的新增内容,我选择为三角函数开设一个实现Factor接口的类Tri,为递推函数的处理单独开设一个FuncHandler类。
因为三角函数的加入导致化简逻辑更加复杂,我修改了Poly类中存储Mono的方法。不再使用第一次作业中采用的ArrayList,而是改为HashMap,将Mono标准化(去除系数)作为键,其原系数作为值。单项式的形式相应地变化为:
$$
\text{Mono}=x^b*\Pi \space\text{Tri}^i
$$
在研讨课上,我发现同学们关于函数的实现方式主要有两种:字符串替换和文法解析。从FuncHandler中callFunction方法的参数可以看出,我选择了前者。这是因为我在完成第二次作业时把函数处理分为两部分:解析与调用,而解析递推函数时只需要不断把形参替换为实参即可,我的程序在这一阶段不需要搞懂函数其他的内容。因此,我选择了字符串替换的方法,有效地实现了指导书需求。
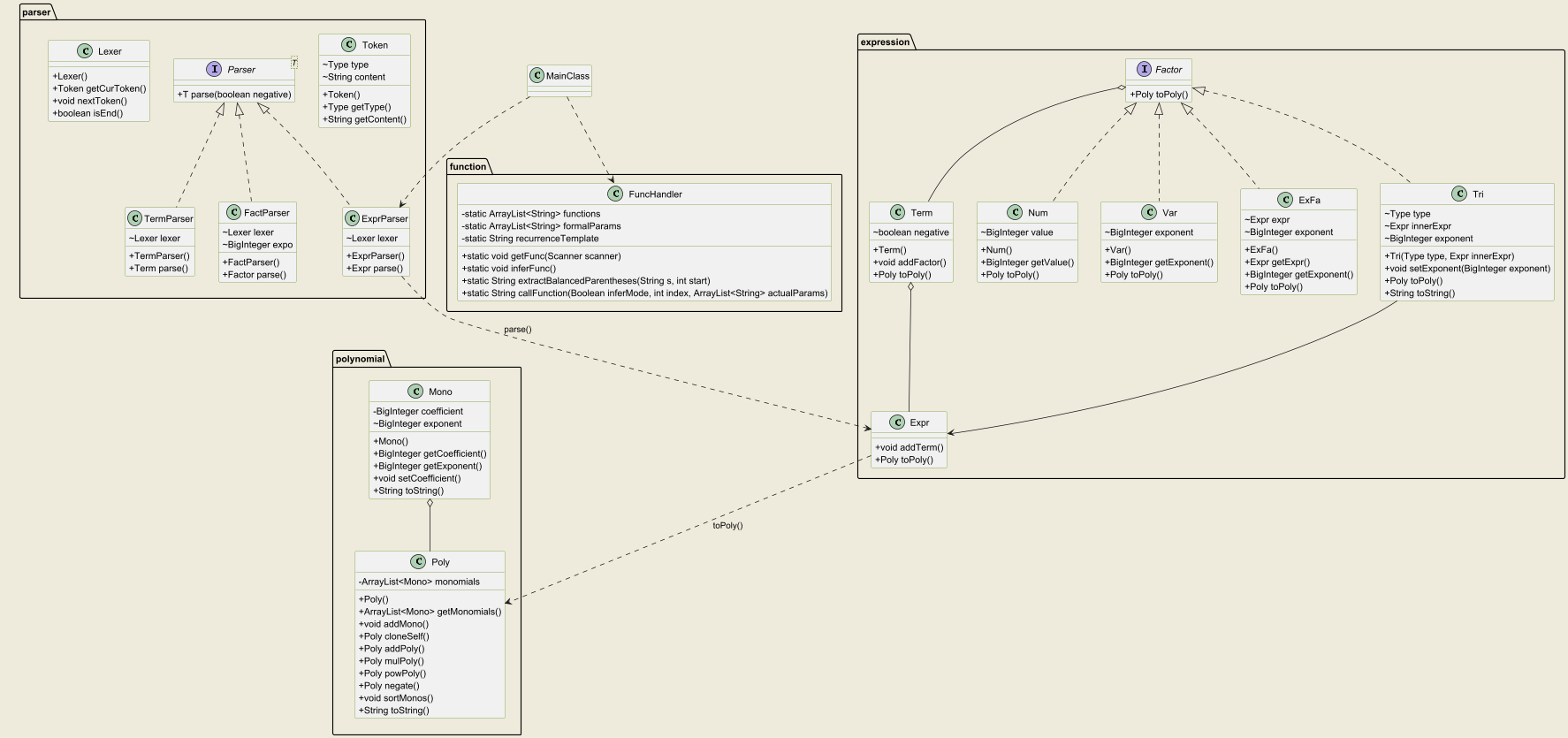
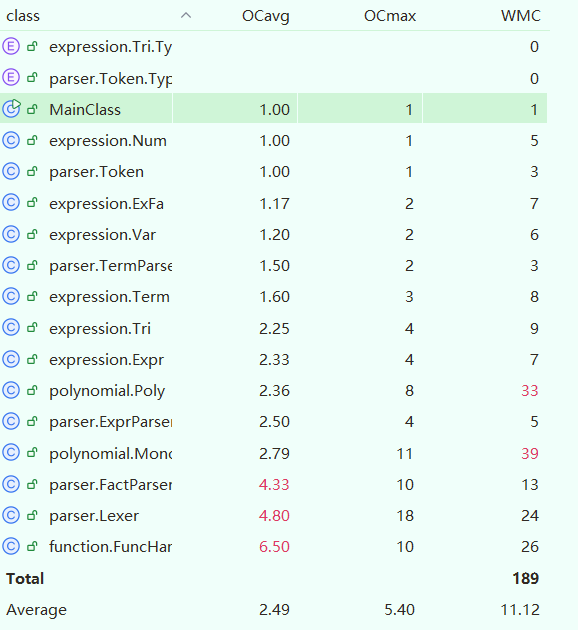
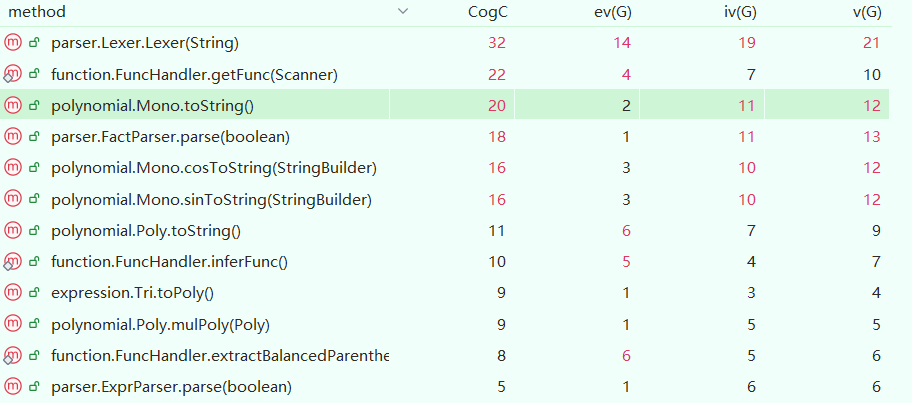
我在本次作业有意识地提炼了FactParser中parse方法的共性代码,在添加新Tri类的前提下仍一定程度地降低了复杂度。但是函数和三角的加入造成了Mono类toString方法的复杂化,是本次作业的复杂度重灾区。
依靠字符串替换,我会在程序开始时推导0~5层函数的表达式,以备后续使用。这导致了FuncHandler类复杂度较高,如果重新设计,我会将部分功能拆分开来,开设多个类来处理函数。此外,提前推导的做法其实是有优化空间的,比如可以等到读取待化简表达式时记录被使用的最高层递推函数,以防无效推导。
第三次作业
在第三次作业中,我的架构仍然保持稳定,没有经历大的调整。我选择为求导操作开设一个实现Factor接口的类Deri,而普通函数与递推函数一样放置在FuncHandler中处理。
到了这一阶段,按理说迭代开发的工作量应该较小。但是我因为在第二次作业中选择了字符串替换的方法处理函数,在第三次作业中遇到了不小的麻烦,主要困难发生在处理多参数的情况。第二次作业中,我们只需通过寻找逗号分割各参数,而进入第三次作业,包含逗号的普通函数也可作为实参,导致旧方法不再适用。在此情况下,我只好又混合了一些parser文法解析的方法,导致最终处理逻辑不太清晰。
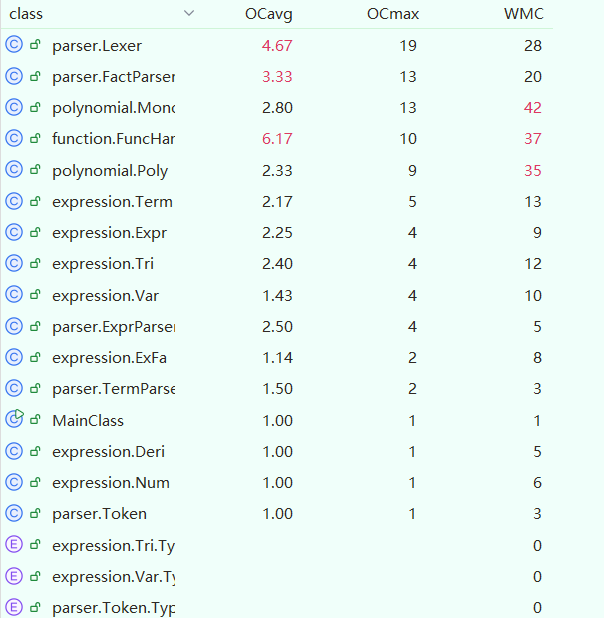
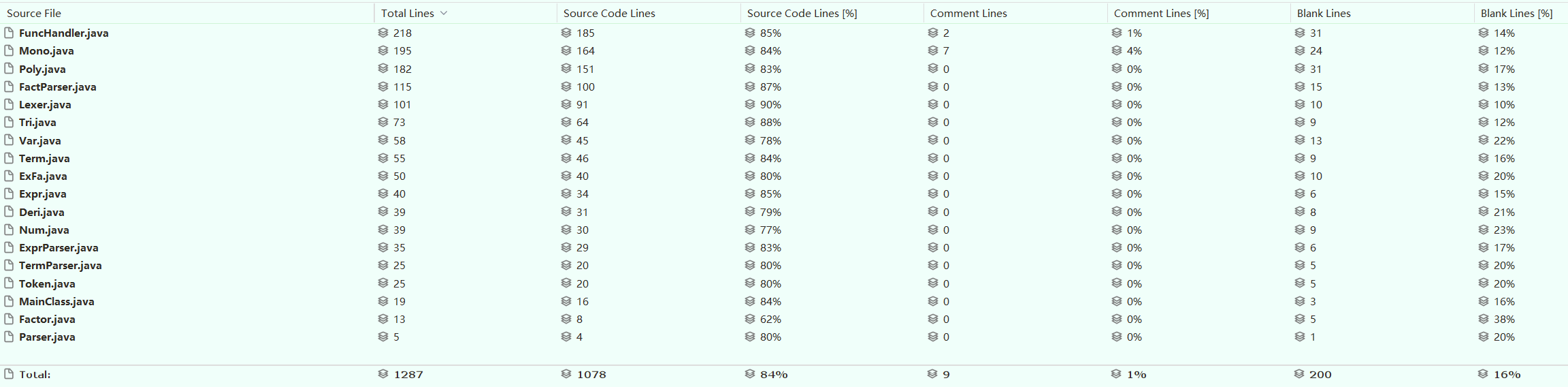
经过进一步简化,Lexer和FactParser的复杂度又有一定程度的下降。最终,我在本单元作业中形成了约1300行代码总量的程序。
假想迭代情境
如果新增求高阶导的需求,求导算子的形式化表述改为:
求导算子 → ’d’ 阶数 ‘x’
阶数 → [’+’] 允许前导零的整数(注:阶数一定是正数)
则我的架构可以从Deri类入手,添加成员变量order来表示求导因子的阶数。相应地,调整toPoly方法为多重循环,调用内部表达式的toDerivative方法,并将得到的结果作为新的内部表达式,再次求导,以此类推。
bug分析
自己代码
本单元共出现3处bug,均出现在第二次作业。
-
0^0处理:在第二次作业中忽略了三角函数为底数的情况,导致形如sin((0-0))^0的表达式被化简为0。该bug出现在新增的三角函数类
Tri,我选择先将三角函数内表达式化简,如果为0则根据三角函数类型特判整体值为0或1。出现此bug的原因是在迭代过程中没有处理好特殊判断,且对拍测试不足。 -
三角函数内缺少必要的括号。
该bug出现在
Mono中的toString方法中,当转化三角函数时内部表达式只有一个单项式就默认不添加括号,这会导致多种错误输出,如sin(-x)和sin(7*x)。其实后者在中测里就有出现,给我的代码造成了bug,但我只是把这一情况修了,并没有考虑全所有情况,很可惜错过了捕捉这个bug的机会。 -
缺少输出。
该bug也出现在
Mono中的toString方法。为了优化长度,很容易想到的一个做法是当系数为正负1时省略系数,但是当变量x及三角函数的指数均为0时,又不能省略。在第一次作业中,条件判断较为简单;进入第二次作业,将三角函数带来的不同情况使我遗漏了部分情况,导致有的时候应该输入1而没有输出。
此外,还有一处运行超时的问题:我的代码在遇到多层三角函数嵌套的情况会出现运行时间过长的问题,在第二次作业中侥幸逃过了互测;然而,我高估了第三次作业互测对cost限制下调的力度,认为我不需要特别解决这个问题,最终还是在互测中被定点爆破。
这个问题是反复调用toString方法导致的,很自然地想到可以添加一个类似cache的成员变量cacheString,如果后续没有发生修改,第一次调用toString之后就可以通过cacheString直接获取结果,极大地提高了效率。
我对比分析了出现bug的方法和未出现bug的方法的度量信息,并未发现明显的行数和复杂度差异。
同学代码
在查找他人程序bug的过程中,除了使用评测机(感谢我的舍友吴震宏提供了强力评测装置!)堆测试量,我借鉴了学长在博客中提到的思路:测试sympy不会检测的格式错误+构造高强度极端数据。
我认为拿到同房间同学的代码就开始通读找bug的做法不是很可行,用评测机堆测试量的方法可以很快地找到代码中明显的bug;而要找出隐藏bug,还是需要按照上面提到的两个思路针对性测试。比如,如果发现其他人的代码有较多三角函数化简,可以考虑从运行效率的角度构造复杂嵌套的数据。
优化
考虑到进行三角函数化简需要投入大量时间,还有影响正确性的可能,我几乎没有进行三角函数方面的优化。
主要实现的优化就是合并同类项和特判三角函数内表达式为0的情况,这两种优化对于代码简洁性的影响很小,因为本身判断条件较为简单;对正确性本应也没什么影响,但是因为我自己的疏忽导致第二种优化在处理0^0时出现bug,很不应该。
心得体会与未来方向
通过本单元的学习,我深化了对于递归下降思想的认识,实现了从上个学期先导课的一知半解到深入本质进行探究。此外,在更大体量的程序实践中,体会了从架构设计到优化迭代的全流程。期间经历了因为函数处理方法选择不当导致的痛苦,也有解决问题跑通程序的喜悦。
本单元的第二次作业的测试很不充分,也给我敲响了警钟,提醒我应该重视本地的多样测试。
未来,希望OO第一单元能够为同学们自行开发cost计算器提供更大力度的支持和一定程度的引导。我在第一次作业一度有编写这个工具的意愿,但是第一次互测全房间都无人刀中让我感觉这个工具不太必要,最后没有坚持下去。
现在想来,编写cost计算器的过程既能督促自己认真研读指导书中的相关定义,了解合法数据的强度范围,又可以从另一角度认识递归(毕竟计算器也应该是通过递归计算整个表达式cost吧),如果当时坚持下去会有更多收获!